Назад

Олимпиадная задача по планиметрии для 9-10 классов: прямая MN и дуга DE в треугольнике

Задача 211860 • Сложность: 3 • 9-10 класс
Задача

Окружность проходит через вершины B и C треугольника ABC и пересекает стороны AB и AC в точках D и E соответственно. Отрезки CD и BE пересекаются в точке O. Пусть M и N – центры окружностей, вписанных соответственно в треугольники ADE и ODE. Докажите, что середина меньшей дуги DE лежат на прямой MN.

Авторы:
Исаев М.
Разделы:
Планиметрия
Источники:
Олимпиады и турниры Всероссийская олимпиада по математике 2006-2007 Региональный этап 10 Класс
Количество версий:
4
Решение
                 
Середину меньшей дугиDEобозначим черезK. Тогда  ∠MEK= ∠MED– ∠KED= ∠MED– ∠KCD= ½ ∠AED– ½ ∠ECD= ½ ∠CDE= ∠EDN  (в частности, точкаKлежит внутри углаMED, так как  ∠MED> ∠KED).   Аналогично  ∠MDK= ∠DEN.  Пусть прямыеDKиEKпересекают описанную окружность треугольникаDEMсоответственно в точкахPиQ(рис. справа). Так как  DK = EK,  то  ∠KED= ∠KDE= ∠PDE= ∠PQE,  откуда PQ || DE.  Далее,  ∠QPM= ∠QEM= ∠KEM= ∠EDN  и аналогично  ∠PQM= ∠DEN. Отсюда вытекает, что треугольникиDENиPQMгомотетичны, причёмKявляется центром гомотетии (как точка пересечения прямыхQEиPD). Следовательно,MNпроходит черезK.
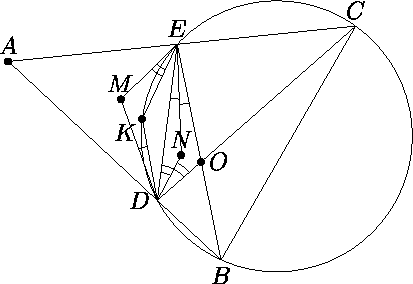
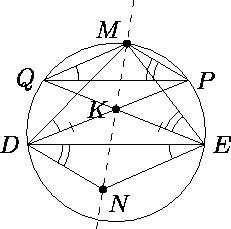
Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет