Олимпиадная задача Исаева М.: докажите неравенство для упорядоченных чисел (9–11 классы)
Задача
Числа x1, x2, ..., xn таковы, что x1 ≥ x2 ≥ ... ≥ xn ≥ 0 и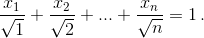 
Докажите, что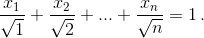 
Решение
Первый способ. Поскольку x1 ≥ ... ≥ xk, для произвольного k имеем
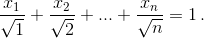откуда 
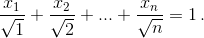и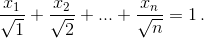 
Значит, 
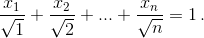Второй способ. Согласно задаче 161388
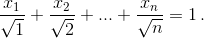
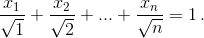
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет