Назад

Олимпиадная задача по планиметрии: точка в равнобедренном треугольнике, классы 7–9

Задача 211792 • Сложность: 2 • 7-9 класс
Задача

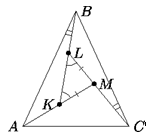
Внутри равнобедренного треугольника ABC  (AB = BC)  выбрана точка M таким образом, что  ∠AMC = 2∠B.  На отрезке AM нашлась такая точка K, что

∠BKM = ∠B.  Докажите, что  BK = KM + MC.

Авторы:
Берлов С. Л.
Разделы:
Планиметрия
Источники:
Олимпиады и турниры Всероссийская олимпиада по математике 2006-2007 Региональный этап 8 Класс
Количество версий:
5
Решение
Продлим отрезокCMдо пересечения сBKв точкеL. По теореме о внешнем угле треугольника  ∠KLM= ∠AMC– ∠BKM= ∠B,  откуда  MK = ML. ∠LCB= ∠KLM– ∠LBC= ∠B– ∠KBC= ∠ABK,  ∠BAK= ∠BKM–ABK= ∠KLM– ∠BCL= ∠LBC;  поэтому треугольникиABKиBCLравны. Значит, BK = CL = CM + ML = CM + MK.
Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет