Олимпиадная задача по математике: цепочка простых чисел и делимость (7–9 класс, Сендеров В. А.)
Задача
Существуют ли такие простые числа p1, p2, ..., p2007, что 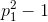 делится на p2,
делится на p2,
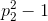 делится на p3, ...,
делится на p3, ..., 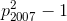 делится на p1?
делится на p1?
Решение
Предположим, что такие числа существуют. Пусть одно из чисел равно 2, скажем, p1 = 2. Тогда последовательно получаем, что p2 = 3, p3 = 2,
p4 = 3, p5 = 2, ..., p2007 = 2, p1 = 3. Противоречие.
Пусть все числа – нечётные простые, и p1 – наибольшее из них. Пусть p2007 = q ≤ p1. Тогда q² – 1 = 2·2·q–1/2·q+1/2, где все сомножители целые и не превосходят q+1/2 < q ≤ p1. Но это противоречит с тому, что q2 – 1 делится на p1.
Ответ
Не существуют.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет