Олимпиадная задача по планиметрии для 7–9 классов: равенство отрезков в четырёхугольнике
Задача
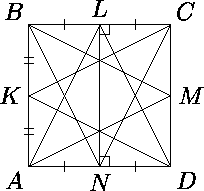
В выпуклом четырёхугольнике семь из восьми отрезков, соединяющих вершины с серединами противоположных сторон, равны.
Докажите, что все восемь отрезков равны.
Решение
Предположим, что восьмой отрезок не равен остальным, и это отрезок CK, где ABCD – данный четырёхугольник, а точки K, L, M, N – середины сторон AB, BC, CD, DA соответственно (см. рис.). Тогда в равнобедренных треугольниках ALD и BNC отрезок LN является медианой, а поэтому и высотой. Далее, прямоугольные треугольники ALN и BNL равны по гипотенузе и катету, отсюда AN = BL, значит, ANLB – прямоугольник. Аналогично DNLC – прямоугольник, и, значит, ABCD – прямоугольник. Из доказанного вытекает, что прямоугольные треугольники DKA и CKB равны по двум катетам, отсюда CK = DK вопреки нашему предположению.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь