Олимпиадная задача по алгебраическим неравенствам и индукции для 9-11 классов
Задача
Для положительных чисел x1, x2, ..., xn докажите неравенство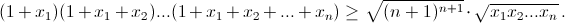 
Решение
Решение 1: Возведя в квадрат, перепишем неравенство в виде 
Обозначим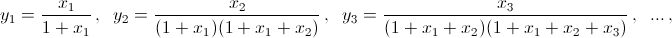 
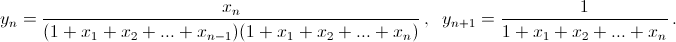
Тогда y1y2...yn+1 = S и
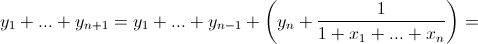
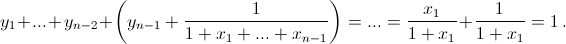По неравенству Коши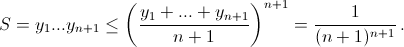 
Решение 2: Применим индукцию. При n = 1 неравенство имеет вид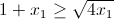 
– частный случай неравенства Коши. Шаг индукции. По предположению индукции для n чисел 
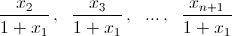верно неравенство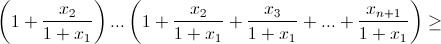 
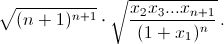
Домножив на (1 + x1)n+1, получаем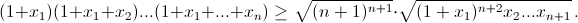 
Осталось показать, что (n + 1)n+1(1 + x)n+2 ≥ (n + 2)n+2x для любого положительного x. По неравенству Коши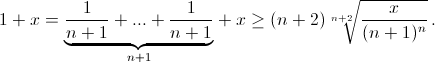 
Возводя в (n+2)-ю степень, получаем требуемое.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет