Олимпиадная задача: биссектриса, медиана и высота в треугольнике — равенство площадей
Задача
Биссектриса, медиана и высота некоторого треугольника, проведённые из трёх разных вершин, пересекаются в одной точке и делят этот треугольник на шесть треугольников (см.рисунок). Площади трёх закрашенных треугольников равны. Верно ли, что исходный треугольник равносторонний?
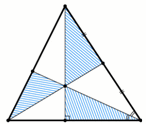
Решение
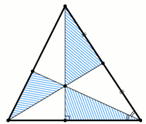
Пусть медиана AK, высота BM и биссектриса CT треугольника ABC пересекаются в точке O. Треугольники BOK и COK равновелики, так как у них равные основания (BK = CK) и общая высота. SCOK = ½ CK·CO sin∠OCK, SCOM = ½ CK·CO sin∠OCM, а так как SCOK = SBOK = SCOM и
∠OCK = ∠OCM, то CM = CK, поэтому треугольники COK и COM равны по двум сторонам и углу между ними. Следовательно,
∠OKC = ∠OMC = 90°, значит, медиана AK треугольника ABC является также его высотой, поэтому треугольник ABC – равнобедренный. Кроме того, из равенства CM = CK = ½BC следует, что в прямоугольном треугольнике BCM катет CM вдвое меньше гипотенузы BC, значит, ∠BCM = 60°. Таким образом, один из углов равнобедренного треугольника ABC равен 60°. Следовательно, этот треугольник – равносторонний.
Ответ
Верно.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь