Олимпиадная задача по планиметрии и стереометрии для 10–11 классов: точки и плоскость
Задача
Точки А1 и А3 расположены по одну сторону от плоскости α, а точки А2 и А4 – по другую сторону. Пусть В1, В2, В3 и В4 – точки пересечения отрезков А1А2, А2А3, А3А4 и А4А1
с плоскостью α соответственно. Найдите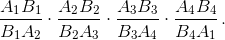 
Решение
Обозначим Сi (i = 1, 2, 3, 4) основания перпендикуляров, опущенных из точек Аi на плоскость α (см. рис.). Прямоугольные треугольники А1С1В1 и А2С2В1 подобны. Следовательно, 
Аналогично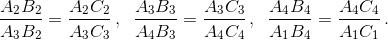 
Почленно перемножая полученные равенства, получим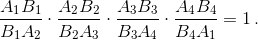 
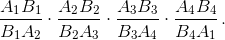
Ответ
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет