Олимпиадная задача Канель-Белова А. Я.: делимость многочленов для 9-11 класса

  Пусть  a² = k(2ab² – b³ + 1)  (k – натуральное число). По условию  2ab² – b³ + 1 > 0,  откуда  a ≥ ^b/₂.  Кроме того,  a² > b²(2a – b).  Следовательно,  a > b  или  2a = b.     (*)

  У уравнения  a² – 2kb²a + k(b³ – 1) = 0  два решения  a₁ ≥ a₂,  причём  a₁a₂ = k(b³ – 1),  a₁ + a₂ = 2kb².  Так как одно из решений – натуральное, то другое – целое неотрицательное. Тогда  a₁ ≥ kb² > 0  и кроме того,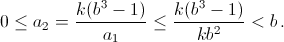  

Из условий (*) получаем, что  a₂ = 0  либо  a₂ = ^b/₂.

  В первом случае  b = 1,  a₁ = 2k.

  Во втором случае, подставляя в уравнение, получаем  b² = 4k.  Значит,  k = n²,  b = 2n,  a₂ = n,  a₁ = 2kb² – a₂ = 8n⁴ – n.

(2n, 1),  (n, 2n),  (8n⁴ – n, 2n),  где n – любое натуральное число.