Олимпиадная задача Канель-Белова на алгебраические неравенства для 9-11 классов
Задача
Определите наименьшее действительное число M, при котором неравенство |ab(a² – b²) + bc(b² – c²) + ca(c² – a²)| ≤ M(a² + b² + c²)² выполняется для любых действительных чисел a, b, c.
Решение
найти наименьшее M, при котором выполнено неравенство |(a – b)(a – c)(b – c)(a + b + c)| ≤ M(a² + b² + c²)². (*)
В силу симметрии без ограничения общности можно считать, что a ≤ b ≤ c. Обозначим c – a = 2t, |a + b + c| = 3s.
Имеем (b – a)(c – b) ≤ ¼ ((b – a) + (c – b))² = t², ((b – a)² + (c – b)²) ≥ ½ ((b – a) + (c – b))² = 2t². Отсюда 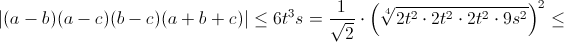

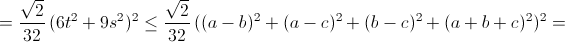
 Итак, неравенство (*) выполняется для
Итак, неравенство (*) выполняется для 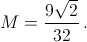 При этом можно достичь равенства, если все неравенства в оценках превратить в равенства (то есть, если b – a = c – b = t и 2t² = 9s²). Это произойдёт, например, при
При этом можно достичь равенства, если все неравенства в оценках превратить в равенства (то есть, если b – a = c – b = t и 2t² = 9s²). Это произойдёт, например, при 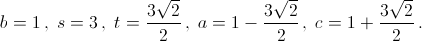 Значит, уменьшить M нельзя.
Значит, уменьшить M нельзя.
Ответ
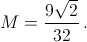
Чтобы оставлять комментарии, войдите или зарегистрируйтесь