Олимпиадная задача по алгебраическим неравенствам для 8-10 классов от Храброва А.
Задача
Известно, что 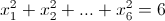 и x1 + x2 + ... + x6 = 0. Докажите, что x1x2...x6 ≤ ½.
и x1 + x2 + ... + x6 = 0. Докажите, что x1x2...x6 ≤ ½.
Решение
Если среди чисел x1, x2, x6 нечётное число отрицательных или есть ноль, то неравенство очевидно.
Пусть отрицательных чисел два или четыре. Меняя, если нужно, знаки у всех чисел, можно добиться того, что ровно два числа будут отрицательными (пусть это x1 и x2). Положим yk = |xk|. Тогда 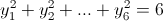 и y1 + y2 = y3 + y4 + y5 + y6. Обозначим последнюю сумму через s . Тогда
и y1 + y2 = y3 + y4 + y5 + y6. Обозначим последнюю сумму через s . Тогда 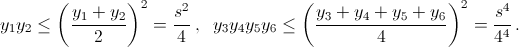 Значит,
Значит, 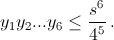 С другой стороны,
С другой стороны,
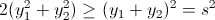 и
и 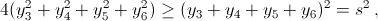 что следует из неравенства между средним арифметическим и средним квадратичным. Таким образом,
что следует из неравенства между средним арифметическим и средним квадратичным. Таким образом, 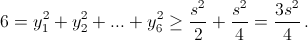
Стало быть, s² ≤ 8 и x1x2...x6 = y1y2...y6 ≤ s6·4–5 ≤ 83·4–5 = ½.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет