Назад

Олимпиадная задача по алгебраическим неравенствам для 9-11 классов от Храброва

Задача 210180 • Сложность: 3 • 9-11 класс
Задача

Докажите, что 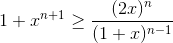    для  x > 0  и натурального n.

Авторы:
Храбров А.
Разделы:
Алгебраические неравенства и системы неравенств
Источники:
Олимпиады и турниры Всероссийская олимпиада по математике 2004-2005 Региональный этап
Количество версий:
5
Решение

Понеравенству Коши 1 +xn+1≥ 2x(n+1)/2,  1 +x≥ 2x½.  Поэтому  (1 +xn+1)(1 +x)n–1≥ 2x(n+1)/2·2n–1x(n–1)/2= 2nxn.  Разделив на  (1 +x)n–1,  получим нужное неравенство.

Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет