Олимпиадная задача: максимальный и минимальный углы выпуклого пятиугольника – доказательство для 7-9 классов

Предположим противное. Рассмотрим пятиугольник ABCDE , удовлетворяющий условиям задачи. Не умаляя общности, можно считать, что угол A – наибольший, а угол D – наименьший (любую пару несмежных вершин можно перевести в эту переобозначениями).

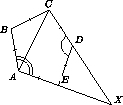
Заметим, что EAC= A- BAC= A- ACB> C- BCA= ACD .

Предположим, что лучи AE и CD пересекаются в точке X . Тогда в треугольнике ACX сторона CX больше стороны AX , так как против нее лежит больший угол. Тогда DX=CX-CD=CX-AE>AX-AE=EX , поэтому180^o- E>180^o- D , что противоречит минимальности угла D .

Случай, когда прямые AE и CD пересекаются с другой стороны от ED , аналогичен. В случае AE|| CD легко прийти к противоречию следующим образом. Заметим, что ACDE – ромб, Δ ABC – равносторонний, и тогда D< E A=60^o+D< C=60^o+ E .

Ответ задачи отсутствует