Олимпиадная задача по теории чисел и алгебре для 9-11 классов от Сендерова В. А.

  Докажем, что числа на окружности не превосходят 2001.   Лемма 1. Пусть x и y – натуральные числа. Если  xy = x + y,  то  x = y = 2,  а если xy < x + y,  то хотя бы одно из чисел x, y равно 1.

  Доказательство. Достаточно переписать неравенство  xy ≤ x + y  в виде  (x – 1)(y – 1) ≤ 1.   Лемма 2. Если  xy = c,  где  x > 0,  y > 0,  x ≤ y,  то сумма  x + y  убывает при возрастании x.

  Доказательство. Это следует из убывания функции 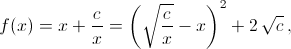    где c > 0,  на интервале 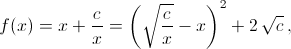    Поделим сумму чисел каждой пары на произведение чисел следующей (по часовой стрелке) пары и перемножим полученные частные. По условию мы получим целое число. С другой стороны, это произведение есть произведение чисел вида  ^a+b/_ab.  Отсюда и из леммы 1 следует, что если хотя бы одна пара отлична от  (2, 2),  то найдётся пара вида  (1, k).  Начнём с этой пары и будем перемещаться по окружности по часовой стрелке.

  Первый случай. Последующие пары имеют вид  (1, k + 1),  (1, k + 2),  ...,  (1, k + 999).  Значит,  k + 1000  кратно k, откуда 1000 кратно k. Но тогда  k ≤ 1000  и  k + 999 ≤ 1999.

  Второй случай. Найдётся такая пара вида  (1, l),  что следующая пара  (a, b)  отлична от  (1, l + 1).  По условию ab – делитель числа s₁ = 1 + l.  Если

ab = l + 1,  то по лемме 2  s₂ = a + b ≤ 2 + ½ (l + 1).    (*)

  Если же  ab ≤ ½ (l + 1),  то по лемме 2  a + b ≤ 1 + ½ (l + 1).  Следовательно, и в этом случае справедливо (*).

  Для следующей пары c, d лемма 2 даёт  s₃ = c + d ≤ cd + 1 ≤ 3 + ½ (l + 1), и т.д. Для суммы s₁₀₀₀ чисел пары, предшествующей  (1, l),  получаем

s₁₀₀₀ ≤ 1000 + ½ (l + 1).

  С другой стороны, s₁₀₀₀ кратно l, значит,  s₁₀₀₀ ≥ l.  Последние два неравенства дают  l ≤ 2001.  Тогда из приведённых выше оценок следует, что для любой пары, отличной от  (1, l),  выполняется неравенство  s ≤ 2001.  Значит, каждое число в этих парах не превосходит 2000.

  Таким образом, оценка 2001 доказана. Из рассуждений легко получить пример:  (1, 2001),  (2, 1001),  (1, 1003),  (1, 1004),  (1, 1005),  ...,  (1, 2000).