Олимпиадная задача по алгебраическим неравенствам для 8–10 классов от Храброва А.
Задача
Для неотрицательных чисел x и y, не превосходящих 1, докажите, что 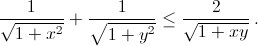
Решение
Возведём доказываемое неравенство в квадрат:
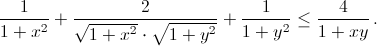
Сначала покажем, что 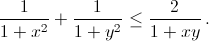
Действительно, после приведения к общему знаменателю и раскрытия скобок имеем
2(1 + x² + y² + x²y²) – (1 + y² + xy + xy³) – (1 + x² + xy + x³y) = (1 – xy)(x – y)² ≥ 0. Согласно неравенству Коши 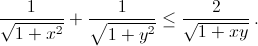
Для завершения доказательства осталось сложить полученные неравенства.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет