Олимпиадная задача по алгебраическим неравенствам: последовательности, 9-11 класс
Задача
В последовательности натуральных чисел {an}, n = 1, 2, ..., каждое натуральное число встречается хотя бы один раз, и для любых различных n и m выполнено неравенство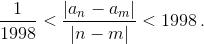 
Докажите, что тогда |an – n| < 2000000 для всех натуральных n.
Решение
Из неравенства в условии следует, что все члены последовательности попарно различны. Лемма. Если i > n и ai < an, то i – n < 2000000.
Доказательство. Отрезок [1, an] содержит лишь конечное число членов последовательности, значит, все ak с достаточно большими номерами k будут больше an. При возрастании индекса от i до бесконечности найдётся такое j, что aj < an < aj+1. Расстояние между aj и aj+1 по условию меньше 1998, поэтому либо an – aj < 999, либо  aj+1 – an < 999. . В первом случае,  |j – n| < 1998(an – aj) < 1998·999, значит, i ≤ j < n + 1998·999 < n + 2·106, во втором аналогично i < j < n – 1 + 1998·999 < n + 2·106. По условию в последовательности встречаются все натуральные числа, значит, an равно числу членов последовательности, лежащих на отрезке [1, an]. Член последовательности, лежащий на отрезке [1, an], имеет индекс не больше n или больше n, количество первых не более n, количество вторых, по доказанному, меньше 2·106. Значит, an < n + 2·106. С другой стороны, также по доказанному, если i < n – 2·106, то ai < an, значит, в отрезке [1, an] содержится больше n – 2·106 членов последовательности. Таким образом, n – 2·106 < an < n + 2·106, откуда |an – n| < 2·106.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь