Олимпиадная задача по делимости многочленов, 8

Олимпиадная задача по делимости и многочленам для 8–10 классов от Тен О.

Задача

Даны натуральные числа m и n. Докажите, что число 2ⁿ – 1 делится на число (2^m – 1)² тогда и только тогда, когда число n делится на число m(2^m – 1).

Решение

2^km – 1 делится на 2^m – 1, поэтому 2^km+d – 1 = 2^km+d – 2^d + 2^d – 1 = 2^d(2^km – 1) + 2^d – 1 ≡ 2^d – 1 (mod 2^m – 1). Таким образом 2ⁿ – 1 делится на 2^m – 1 тогда и только тогда, когда n делится на m. Если n = km, то 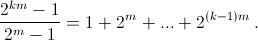Каждое слагаемое дает остаток 1 при делении на 2^m – 1, поэтому 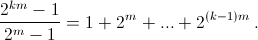Значит, 2^km – 1 делится на (2^m – 1)² тогда и только тогда, когда k делится на 2^m – 1, что равносильно тому, что n делится на m(2^m – 1).