Олимпиадная задача по алгебре: доказательство неравенства для a и b (8–10 класс)
Задача
Докажите, что если 0 < a, b < 1, то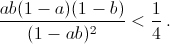 
.
Решение
Пусть ab = u², a + b = v. Учитывая, что v ≥ 2u (неравенство Коши), получаем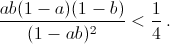 
так как u/u+1 < ½ ⇔ u = 1.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет