Назад

Олимпиадная задача о фишке на шестиугольнике: планиметрия и комбинаторная геометрия

Задача 209895 • Сложность: 3 • 7-9 класс
Задача
В одном из узлов шестиугольника со стороной n , разбитого на правильные треугольники (см. рис.) , стоит фишка. Двое играющих по очереди передвигают ее в один из соседних узлов, причем запрещается ходить в узел, в котором фишка уже побывала. Проигрывает тот, кто не может сделать хода. Кто выигрывает при правильной игре?
Решение
Выигрывает второй.

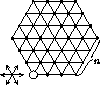
Разобьем все узлы решетки, кроме того, который фишка занимает в начале игры, на пары соседних. Тогда после каждого хода первого игрока второй может передвинуть фишку в узел, находящийся в паре с только что занятым. Рано или поздно первый игрок окажется в ситуации, когда он не сможет сделать ход. Разбиение на пары приведено на рисунке. Сначала мы разбиваем на пары все узлы, находящиеся на границе решетки, за исключением одного, соседнего с исходной позицией фишки. Оставшийся узел соединяем с узлом, лежащим на отрезке между исходной позицией и центром решетки. После этого узлы, не вошедшие в пары, образуют шестиугольную решетку с выброшенным угловым узлом и стороной, на единицу меньше, чем исходная решетка, и мы повторяем ту же операцию.

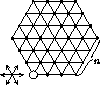
Решетка со стороной 1 разбивается на 3 пары (см. рис.) .
Ответ

Выигрывает второй.

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет