Олимпиадная задача по алгебре: квадратичные функции и наименьшее значение выражения
Задача
Рассматриваются такие квадратичные функции f(x) = ax² + bx + c, что a < b и f(x) ≥ 0 для всех x.
Какое наименьшее значение может принимать выражение a+b+c/b–a ?
Решение
Из условия следует, что a > 0 и b² – 4ac ≤ 0. Обозначим A = a+b+c/b–a. Тогда, в силу неравенства Коши
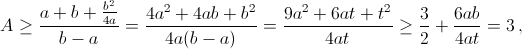 причём равенство A = 3 достигается, если 4ac = b² и t = 3a, то есть при
причём равенство A = 3 достигается, если 4ac = b² и t = 3a, то есть при
b = c = 4a. Соответствующий трёхчлен: ax² + 4ax + 4a = a(x + 2)², где a – произвольное положительное число.
Ответ
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет