Олимпиадная задача по планиметрии: четырёхугольник с вписанной окружностью
Задача
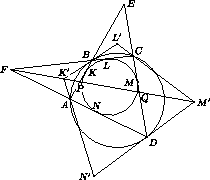
Четырёхугольник ABCD является одновременно и вписанным, и описанным, причём вписанная в ABCD окружность касается его сторон AB, BC, CD и AD в точках K, L, M, N соответственно. Биссектрисы внешних углов A и B четырёхугольника пересекаются в точке K', внешних углов B и C – в точке L', внешних углов C и D – в точке M', внешних углов D и A – в точке N'. Докажите, что прямые KK', LL', MM' и NN' проходят через одну точку.
Решение
Если ABCD– трапеция (скажем, AB || CD), то прямые L'L и N'N имеют общую точку пересечения с серединным перпендикуляром к AB, на котором лежат K, K', M и M'.
Пусть прямые AB и CD пересекаются в точке E, а прямые BC и AD – в точке F (см. рис.).
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет