Олимпиадная задача по алгебраическим неравенствам для 8-10 классов — автор Берлов С. Л.

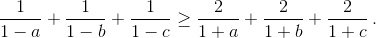
Решение 1:Заметим, что 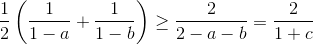    (мы использовали неравенство  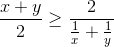   между средним арифметическим и средним гармоническим для положительных x, y). Осталось сложить три аналогичных неравенства.

Решение 2:   Не умаляя общности, можно считать, что  a ≥ b ≥ c,  тогда  1 – c² ≥ 1 – b² ≥ 1 – a²  и, следовательно, 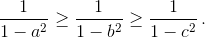    Заметим, что  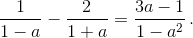   Таким образом, нужно доказать неравенство  

  Поскольку сумма числителей равна 0, неравенство будет доказано, если мы заменим знаменатели на равные таким образом, что каждая дробь при этом не увеличится. Если  a ≥ b ≥ ⅓ ≥ c,  то заменим все знаменатели на  1 – c²,  в результате отрицательное слагаемое не изменится, а положительные не увеличатся. Если  a ≥ ⅓ b ≥ c,  то заменим все знаменатели на  1 – b²,  тогда положительное слагаемое и одно из отрицательных только уменьшатся, а второе отрицательное слагаемое останется неизменным.

Ответ задачи отсутствует