Олимпиадная задача по теории чисел: Докажите возрастание последовательности aₙ (Храбров А., 9-11 класс)
Задача
Последовательность натуральных чисел an строится следующим образом: a0 – некоторое натуральное число; an+1 = ⅕ an, если an делится на 5;
an+1 = [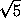 an], если an не делится на 5. Докажите, что начиная с некоторого члена последовательность an возрастает.
an], если an не делится на 5. Докажите, что начиная с некоторого члена последовательность an возрастает.
Решение
Условие эквивалентно тому, что начиная с некоторого n число an не делится на 5. Докажем это.
Покажем, что найдутся два соседних члена последовательности, не кратных 5. Предположим противное. Тогда для любого n либо an+1 получается из an делением на 5, либо an+2 получается из an+1 делением на 5. Заметим, что всегда ak+1 ≤ 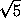 ak , поэтому an+2 ≤ ⅕
ak , поэтому an+2 ≤ ⅕ 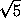 an < an. Это означает, что последовательность натуральных чисел a1, a3, a5, ... строго убывает. Противоречие.
an < an. Это означает, что последовательность натуральных чисел a1, a3, a5, ... строго убывает. Противоречие.
Итак, найдутся ak и ak+1, не делящиеся на 5. Докажем, что ak+2 также не кратно 5. Так же последовательно получим, что ak+3, ak+4, ... не делятся на 5, что и требуется.
ak+1 = [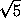 ak], ak+2 = [
ak], ak+2 = [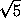 ak+1]. Положим ak = m, тогда ak+1 =
ak+1]. Положим ak = m, тогда ak+1 = 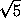 m – α, где 0 < α < 1. ak+2 = [
m – α, где 0 < α < 1. ak+2 = [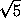 (
(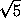 m – α] = 5m + [–
m – α] = 5m + [– 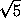 α]. Но поскольку
α]. Но поскольку
0 < 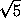 α < 3, то m – 3 ≤ ak+2 < 5m, то есть ak+2 не делится на 5.
α < 3, то m – 3 ≤ ak+2 < 5m, то есть ak+2 не делится на 5.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь