Олимпиадная задача: неравенство для суммы произведений на рёбрах дерева (Дольников В. Л.)

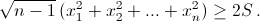
Решение 1:   Рассмотрим ребро l, соединяющее вершины с числами x_i и x_j. Обозначим через k_i(l) число вершин, из которых нельзя пройти в вершину x_i при удалении ребра l.

  Ясно, что   1 ≤ k_i(l), k_j(l) ≤ n – 1,  k_i(l) + k_j(l) = n.  Кроме того, для каждого i сумма 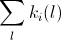    равна  n – 1  (сумма берётся по всем рёбрам l, выходящим из x_i), так как из вершины x_i можно пройти по рёбрам дерева в каждую из оставшихся  n – 1  вершин единственным несамопересекающимся путем.

  Согласно неравенству Коши для данного ребра l получим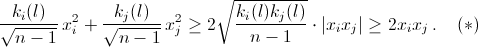  

  Последнее неравенство верно, так как  k_i(l)k_j(l) = ¼ ((k_i(l) + k_j(l))² – (k_i(l) – k_j(l))² ≥ ¼ (n² – ((n – 1) – 1)²) = n – 1.

  Сложив неравенства (*) по всем рёбрам, получим требуемое неравенство.

Решение 2:   Будем проводить операции, не изменяющие чисел в вершинах и не уменьшающие сумму S чисел на рёбрах. Достаточно доказать неравенство по окончании этих операций.

  Вначале заменим числа в вершинах на их модули, то есть далее считаем, что x₁, x₂, ..., x_n ≥ 0.

  Выберем наибольшее из чисел x_i, пусть это число x₁. Если нашлась вершина с числом x_i,  i ≠ 1,  из которой выходит ровно одно ребро l, ведущее в вершину x_j,  j ≠ 1,  то произведём перестройку: удалим ребро l и соединим ребром вершины с числами x_i и x₁. Полученный граф остаётся деревом, так как количество рёбер не изменилось и по-прежнему из каждой вершины можно пройти по рёбрам в любую другую. После перестройки сумма S изменяется на  x_ix₁ – x_ix_j ≥ 0.  Производим перестройки, пока это возможно. Поскольку при каждой перестройке число рёбер, выходящих из вершины с числом x₁, увеличивается, через конечное число шагов мы придём к ситуации, когда невозможно сделать перестройку. Это означает, что вершина с числом x₁ соединена ребром с каждой из оставшихся  n – 1  вершин.

  Таким образом, для конечной ситуации   S = x₁x₂ + x₁x₃ + ... + x₁x_n.  При этом неравенство верно, поскольку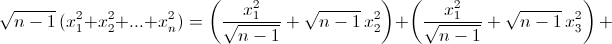      

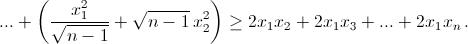
Ответ задачи отсутствует