Олимпиадная задача по теории чисел о делимости для 9-11 класса, Берлов С. Л.
Задача
a и b – такие различные натуральные числа, что
ab(a + b) делится на a² + ab + b². Докажите, что |a – b| > 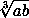 .
.
Решение
Пусть d = НОД(a, b), то есть a = du, b = dv, где u и v взаимно просты. Тогда duv(u + v) делится на u² + uv + v² = m. Число u + v взаимно просто с числами u и v, поэтому из равенств m = u(u + v) + v² = v(u + v) + u² следует, что m взаимно просто с числами u, v и u + v. Значит, d делится на m. Но тогда d ≥ m > uv, следовательно, d³ > ab. Поэтому |a – b| ≥ d > 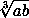 .
.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет