Доказательство алгебраического неравенства для любого n — олимпиадная задача Храброва
Задача
Докажите, что при любом натуральном n справедливо неравенство 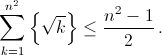
Решение
При n = 1 неравенство обращается в равенство 0 = 0. При n > 1 докажем, что сумма дробных частей на каждом промежутке между двумя последовательными квадратами удовлетворяет неравенству 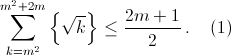 Из неравенства между средним арифметическим и средним квадратичным получаем
Из неравенства между средним арифметическим и средним квадратичным получаем 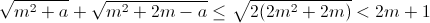 при 0 ≤ a ≤ m.
при 0 ≤ a ≤ m.
Следовательно, 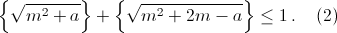
Просуммировав эти неравенства при a = 0, 1, ..., m – 1 и неравенство 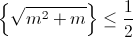 (получаемое делением на 2 обеих частей (2) при a = m), приходим к неравенству (1). Суммируя неравенство (1) по всем m от 1 до n – 1, получаем
(получаемое делением на 2 обеих частей (2) при a = m), приходим к неравенству (1). Суммируя неравенство (1) по всем m от 1 до n – 1, получаем 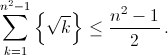
Остаётся заметить, что 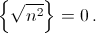
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет