Олимпиадная задача: число удачных расстановок в квадратной таблице 2ⁿ–1 × 2ⁿ–1

Решение 1:   Лемма. Пусть в таблице из  2ⁿ – 1  столбцов и k строк  (k + 1  не кратно 3) числа ±1 расставлены удачно. Тогда все числа в таблице равны единице.   Доказательство. Индукция по n.

  База. При  n = 1  имеем один столбец. Пусть в нем стоят числа a₁, a₂, ..., a_k – по порядку сверху вниз. Тогда  a₁ = a₂  (условие для первой клетки),

a₂ = a₁a₃,  следовательно,  a₃ = 1,  1 = a₃ = a₂a₄,  следовательно,  a₄ = a₂ = a₁.  И так далее: все числа, стоящие в клетках с номером, кратным 3, равны 1, а все остальные равны a₁. Поскольку  k + 1  не кратно 3, то возможны две ситуации:  1) a_k– = a₁,  a_k = 1;   2)  a_k–1 = 1,  a_k = a₁.  Но a_k равен произведению своих соседей, то есть a_k = a_k–1. Следовательно,  a₁ = 1,  и столбец состоит из одних единичек.

  Шаг индукции. Введём следующие обозначения. Если A, B – две таблицы одинакового размера, то пусть A·B – таблица, в каждой клетке которой записано произведение чисел из тех же клеток таблиц A и B. A' – таблица, полученная из A зеркальной симметрией: первый столбец меняется с последним, второй – с предпоследним и так далее. Ясно, что если числа в таблицах A и B расставлены удачно, то это же верно для таблиц A·B и A'. Таблицу, в которой стоят только единицы, будем обозначать 1.

  Докажем, что если в таблице A размера  k×(2ⁿ⁺¹ – 1)  числа расставлены удачно, то расстановка симметрична:  A = A'.  Это равносильно тому, что

A·A' = 1.

  В таблице A·A' весь центральный столбец (с номером 2ⁿ) состоит из единиц, так как центральные столбцы у A и A' одинаковы. Следовательно, если мы рассмотрим отдельно часть таблицы A·A' слева от центрального столбца, то в этой меньшей таблице числа расставлены удачно. Размер её –  k×(2ⁿ – 1),  так что по предположению индукции все числа в ней – единицы. То же касается и правой части A·A'. Итак,  A·A' = 1.

  Значит, для каждого числа из центрального столбца таблицы A числа слева и справа от него одинаковы, поэтому само оно равно произведению своих верхнего и нижнего соседей.

  Как показано выше, из этого следует, что центральный столбец заполнен единицами. Теперь снова рассмотрим часть таблицы A слева от центрального столбца. Применяя предположение индукции, убеждаемся, что в ней стоят только единицы. Правая часть симметрична левой, поэтому и она состоит из единиц.   Итак, для всех таблиц размера  k×(2ⁿ – 1),  где  k + 1  не кратно 3, единственна. В частности, она единственна при  k = 2ⁿ – 1,  потому что  k + 1 = 2ⁿ.

Решение 2:   Пусть R – удачная расстановка в таблице (2ⁿ – 1)×(2ⁿ – 1). Расставим числа на клетчатой плоскости, как показано на рисунке слева (симметрия буквы R означает, что там стоит таблица R, отраженная соответствующим образом). Тогда расстановка на всей плоскости удачна (то есть любое число есть произведение его четырёх соседей) и, кроме того, она 2ⁿ⁺¹-периодична, то есть при сдвиге на 2ⁿ⁺¹ вверх или вправо она переходит в себя.

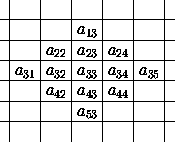
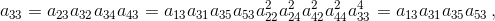  Докажем индукцией поn, что любая 2ⁿ-периодичная перестановка состоит из единиц.  База (n= 0)  очевидна:  a = a⁴,  гдеa– число в клетке.  Шаг индукции. Пусть  n≥ 1.  Рассмотрим фрагмент таблицы, показанный на рисунке справа.   Имеем:  a₂₃=a₁₃a₂₂a₂₄a₃₃, a₃₂=a₂₂a₃₁a₃₃a₄₂, a₃₄=a₂₄a₃₃a₃₅a₄₄, a₄₃=a₃₃a₄₂a₄₄a₅₃,  откуда   то есть то же соотношение верно для "разрежённой" таблицы, состоящей из чисел, находящихся в пересечениях нечётных строк с нечётными столбцами. Эта таблица 2^n–1-периодична, поэтому по предположению индукции она состоит из единиц. Аналогично остальные три "разрежённых" подтаблицы состоят из единиц, что и требовалось.

Удачная расстановка единственна – все числа равны единице.