Олимпиадная задача: радиус окружности внутри параболы y = x² (Многочлены, планиметрия)
Задача
Внутри параболы y = x² расположены несовпадающие окружности ω1, ω2, ω3, ... так, что при каждом n > 1 окружность ωn касается ветвей параболы и внешним образом окружности ωn–1 (см. рис.). Найдите радиус окружности σ1998, если известно, что диаметр ω1 равен 1 и она касается параболы в её вершине.
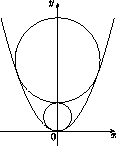
Решение
Докажем по индукции, что радиус rn окружности ωn равен n – ½, а её центр – точка (0, n² – n + ½). База дана в условии.
Шаг индукции. Верхняя точка окружности ωn имеет ординату n² – n + ½ + n – ½ = n². Поэтому центр окружности ωn+1 радиуса n + ½, касающейся σn в верхней точке имеет координаты (0, n² + n + ½). Значит, уравнение окружности σn+1 имеет вид
x² + (y – n² – n – ½)² = (n + ½)² или x² + (y – n²)² – 2(y – n²)(n + ½) = 0. Подставляя в него y вместо x², получим
y – n² + (y – n²)² – 2(y – n²)(n + ½) + n² = 0, то есть (y – n² – n)² = 0. Таким образом, это уравнение имеет единственное решение y = n² + n. Следовательно, окружность ωn+1 имеет с параболой y = x² ровно две общие точки (с указанной ординатой). Это и значит, что она касается параболы.
Ответ
r1998 = 1997,5.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь