Олимпиадная задача по планиметрии для 9-11 классов: свойства выпуклого многоугольника
Задача
Выпуклый многоугольник M переходит в себя при повороте
на угол90o . Докажите, что найдутся два круга с отношением радиусов,
равным 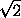 , один из которых содержит M , а другой содержится
в M .
, один из которых содержит M , а другой содержится
в M .
Решение
Пусть O – центр поворота, R – наибольшее из расстояний
от точки O до вершин многоугольника, A1 – одна из вершин,
такая, что OA1=R . Если A1 переходит при повороте в вершину A2 , A2 – в A3 , A3 – в A4 , то, очевидно, A1A2A3A4 – квадрат с центром в точке O ; этот квадрат,
очекидно, лежит в M . Отношение радиусов его вписанного и описанного
кругов равно 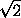 , при этом первый лежит в M , а второй содержит M по определению R , что и требовалось.
Справедливо следующее утверждение: если выпуклый многоугольник M переходит в себя при повороте на угол α ( α<180o ), то найдутся два круга с отношением радиусов,
равным 2, один из которых содержит M , а другой содержится в M .
Попробуйте доказать его самостоятельно.
, при этом первый лежит в M , а второй содержит M по определению R , что и требовалось.
Справедливо следующее утверждение: если выпуклый многоугольник M переходит в себя при повороте на угол α ( α<180o ), то найдутся два круга с отношением радиусов,
равным 2, один из которых содержит M , а другой содержится в M .
Попробуйте доказать его самостоятельно.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь