Олимпиадная задача по алгебраическим неравенствам: неравенство для квадратного трехчлена

Решение 1:   Пусть  P(x) = ax² + bx + c.  Тогда

     (P(xy))² – P(x²)P(y²) = (ax²y² + bxy + c)² – (ax⁴ + bx² + c)(ay⁴ + by² + c) =

        = a²x⁴y⁴ + b²x²y² + c² + 2abx³y³ + 2acx²y² + 2bcxy – a²x⁴y⁴ – b²x²y² – c² – abx²y²(x² + y²) – ac(x⁴ + y⁴) – bc(x² + y²) =

           = abx²y²(2xy – x² – y²) + ac(2x²y² – x⁴ – y⁴) + bc(2xy – x² – y²) = – abxy²(x – y)² – ac(x² – y²)² – bc(x – y)² ≤ 0.

Решение 2:   Докажем, что утверждение задачи справедливо для произвольного многочлена с неотрицательными коэффициентами.

  Пусть 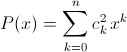    (любое неотрицательное число является квадратом). Тогда неравенство (P(xy))² ≤ P(x²)P(y²)  запишется в виде  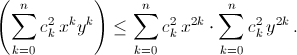   Обозначив  a_k = c_kx^k,  b_k = c_ky^k,  мы сведём задачу к известному неравенству Коши–Буняковского (см. задачу 161402 а).

Ответ задачи отсутствует