Математическая задача: конечные множества и многочлены

Задача

Существует ли такое конечное множество M ненулевых действительных чисел, что для любого натурального n найдется многочлен степени не меньше n с коэффициентами из множества M, все корни которого действительны и также принадлежат M?

Решение

Пусть M = {a₁, a₂, ..., a_k} – произвольное множество ненулевых чисел, m = min {|a₁|, |a₂|, ..., |a_k|}, M = max {|a₁|, |a₂|, ..., |a_k|}. Тогда M ≥ m > 0. Рассмотрим многочлен P(x) = b_nxⁿ + b_n–1x^n–1 + ... + b₁x + b₀, все коэффициенты b₀, b₁, ..., b_n и корни x₁, x₂, ..., x_n которого принадлежат множеству M. По теореме Виета 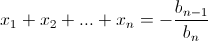и 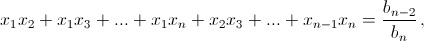поэтому 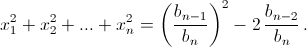Отсюда 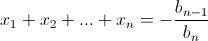то есть 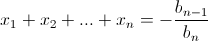Значит, при n > A нужного многочлена не существует.