Олимпиадная задача по планиметрии: стороны выпуклого многоугольника, классы 9–11

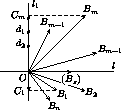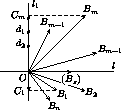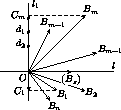Пусть A_nA₁ – самая короткая (одна из них) сторона многоугольника A₁A₂.. A_n с равными углами. Тогда A_nA₁ A₁A₂ и A_nA₁ A_n-1A_n . Предположим, что многоугольник не имеет других, кроме A_nA₁ сторон, не превосходящих соседних с ними. Пусть A_mA_m+1– самая длинная (одна из них) сторона многоугольника. Тогда A_nA₁1A₂2A₃<..mA_m+1, так как если A_k-1A_k A_kA_k+1, то наименьшая среди сторон A_kA_k+1, A_m-1A_m не длиннее соседних с ней. Аналогично A_nA₁n-1A_n<..m+1A_m+2mA_m+1.

Отложим векторы 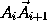, i=1, n от одной точки: 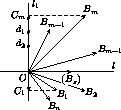= 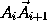1041. Тогда +...+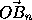=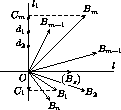+...+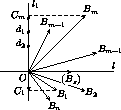= 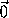, и, следовательно, сумма проекций 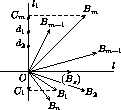, i=1, n , этих векторов на любую прямую l₁ равна 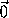. Возьмем в качестве l₁ прямую, перпендикулярную биссектрисе l угла B₁OB_m . Из условия следует, что 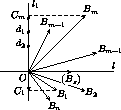B₁OB₂=..= 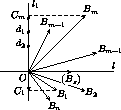B_m-1OB_m= 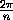, поэтому пары лучей[OB₁)и[OB_m),[OB₂)и[OB_m-1), симметричны относительно прямой l . Для нечетного m , m=2s-1, без пары останется луч[OB_s), лежащий на l . Соответственно, векторы 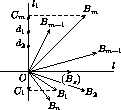i=1, m , разобьются на пары противоположно направленных векторов, причем OC₁<OC_m , OC₂<OC_m-1, (если m=2s+1, то 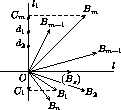= 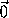). 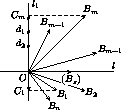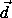Таким образом, +...+=₁ , где 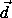₁ – направленный вверх вектор. Аналогично, 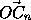++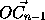...+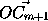=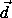₂ , где 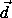₂ сонаправлен с 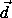₁ и хотя бы один из векторов 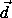₁ и 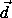₂ ненулевой. 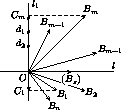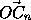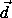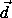Но тогда +...+=₁+₂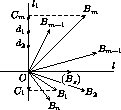 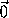. Противоречие, следовательно найдется отличная от A_nA₁ сторона многоугольника, не превосходящая соседние с ней стороны.

Ответ задачи отсутствует