Олимпиадная задача: Решить уравнение с вложенными тригонометрическими функциями (Сендеров В. А., Ященко И. В.)

Корней нет. Покажем, что при всех x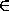 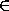справедливо неравенство

cos(cos(cos(cos x)))> sin(sin(sin(sin x))). (1)

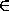Достаточно это доказать для x[0,2π ]. Если x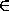[π ,2π ], то утверждение очевидно: для таких x выполнено cos(cos(cos(cos x)))>0, а sin(sin(sin(sin x)))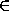0.

Пусть x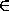 [0,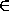]. Тогда каждое из чисел cos x , sin x , cos(cos x) , sin(sin x) , cos(cos(cos x)) , sin(sin(sin x)) неотрицательно и не превосходит 1. Так как всегда sin x+ cos x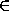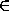< 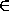, то для рассматриваемых значений x выполняются неравенства0 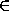cos x<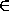- sin x . Следовательно,

cos(cos x)> cos (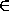- sin x)= sin(sin x), (2)

sin(cos x)< sin (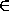- sin x)= cos(sin x). (3)

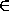Из (2) получаем, что cos(cos(cos x))< cos(sin(sin x)) , поэтому cos(cos(cos x))+ sin(sin(sin x))< cos( sin(sin x))+ sin( sin(sin x))< , откуда cos(cos(cos x))<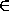- sin(sin(sin x)) и, следовательно,

cos(cos(cos(cos x)))> cos(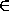- sin(sin(sin x)))= sin(sin(sin(sin x))).

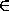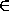Пусть x (;π ). Положим y=x- 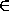, тогда y 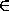(0,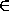), и неравенство (1) принимает вид

cos(cos(cos(sin y)))> sin(sin(sin(cos y))). (1')

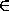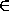Так как при y (0,)каждое из чисел cos sin y и sin cos y также принадлежит интервалу(0,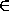), то в силу (2) получаем, что cos(cos( cos(sin y)))> sin(sin( cos(sin y))) . Функция sin(sin t) , t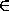(0,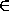), является возрастающей, поэтому в силу (3) имеем

sin(sin( cos sin y))> sin(sin( sin cos y)).

Неравенство(1')(а вместе с ним и неравенство (1)) доказано.

Корней нет.