Назад

Олимпиадная задача по планиметрии и числовым последовательностям для 9–11 классов от Канель-Бёлов А. Я.

Задача 209598 • Сложность: 4 • 9-11 класс
Задача

На плоскости отмечены две точки на расстоянии 1. Разрешается, измерив циркулем расстояние между двумя отмеченными точками, провести окружность с центром в любой отмеченной точке с измеренным радиусом. Линейкой разрешается провести прямую через любые две отмеченные точки. При этом отмечаются новые точки – точки пересечения построенных линий. Пусть Ц(n) – наименьшее число линий, проведение которых одним циркулем позволяет получить две отмеченные точки на расстоянии n (n – натуральное). ЛЦ(n) – то же, но циркулем и линейкой. Докажите, что последовательность 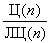   неограничена.

Авторы:
Канель-Белов А. Я.
Разделы:
Планиметрия Числовые последовательности
Источники:
Олимпиады и турниры Всероссийская олимпиада по математике 1994-1995 Заключительный этап
Количество версий:
5
Решение

  1) Если d – наибольшее из расстояний между отмеченными точками, то проведение одной линии циркулем позволяет получить отмеченную точку на расстоянии не более 2d от уже отмеченных. Отсюда следует, что  Ц(2n) ≥ n,  а значит,  Ц(22n) ≥ 2n.

  2) Пусть A и B – две данные отмеченные точки. Проведение пяти линий позволяет построить угол BAC, где  AC = 2  (рис. слева).

         
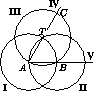
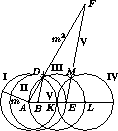
  Покажем, что проведение пяти линий позволяет построить отрезок длиныm², если уже получен отрезок длиныm(рис. справа).   Последовательно строим окружности σ1, σ2, σ3, σ4радиусаmс центрами в точкахA, B, K– точке пересечения σ1сAB, L– точке пересечения σ3сABи, наконец, прямуюEM, гдеE– точка пересечения σ2сAB, M– точка пересечения σ3с σ4.   ПустьF– точка пересеченияEMсAC, аD– точка пересечения σ1с σ3, лежащая на лучеAC. ТреугольникиADKиKML– равносторонние со сторонами AD = KM = m,  ∠DAB= ∠MKE= 60°, AB = KE= 1,  поэтому ∠DBA= ∠MEK,  следовательно,  EM || BD.  По теореме Фалеса  AB:AD = BE:DF,  откуда следует, что  DF = m².  Таким образом,  ЛЦ(2) ≤ 5,  ЛЦ(4) ≤ 2·5,  ЛЦ(22n) ≤ 5(n+ 1).   3) Теперь утверждение задачи очевидно.
Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет