Олимпиадная задача по делимости и степеням: доказательство делимости выражения на 8 для любого n > 2
Задача
Докажите, что для любого натурального n > 2 число
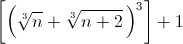делится на 8.
Решение
Утверждение будет доказано, если мы покажем, что при n ≥ 3 справедливо равенство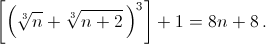 
Для этого достаточно показать, что при n ≥ 3 справедливы неравенства 
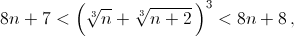то есть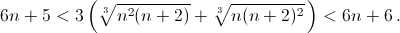 
Правое неравенство следует из того, что n²(n + 2) < (n + ⅔)³ и n(n + 2)² < (n + 4/3)³. Левое неравенство следует из того, что 
и n(n + 2) > (n + ⅚)² при n > 5/12, то есть при n ≥ 3.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет