Олимпиадная задача про перекраску точек в пятиугольнике: теорема о диагоналях и инварианты
Задача
В выпуклом пятиугольнике проведены все диагонали. Каждая вершина и каждая точка пересечения диагоналей окрашены в синий цвет. Вася хочет перекрасить эти синие точки в красный цвет. За одну операцию ему разрешается поменять цвет всех окрашенных точек, принадлежащих либо одной из сторон либо одной из диагоналей на противоположный (синие точки становятся красными, а красные – синими). Сможет ли он добиться желаемого, выполнив какое-то количество описанных операций?
Решение
Рассмотрим внутренний пятиугольник, образованный точками пересечений диагоналей исходного пятиугольника (cм. рис.).
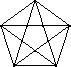
Ответ
Не сможет.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет