Олимпиадная задача по планиметрии для 8-9 классов: точка M и медиана треугольника
Задача
Точка M лежит на стороне BC треугольника ABC . Известно, что радиус окружности, вписанной в треугольник ABM , в два раза больше радиуса окружности, вписанной в треугольник ACM . Может ли отрезок AM оказаться медианой треугольника ABC ?
Решение
Пусть АМ = m – медиана треугольника ABC , p1 и r – полупериметр и радиус окружности, вписанной в треугольник ACM , а p2 и2r – полупериметр и радиус окружности, вписанной в треугольник AВM (см. рис. 11.3).
Площади треугольников ABM и AСM равны, следовательно p1· r = p2· 2r , то есть p1 = 2p2 . Получим: 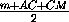 =m+AB+BM . Так как BM = CM , то АС = m + 2AB + CM > m + CM . Это противоречит
неравенству треугольника для ΔAMC : АС < m + CM .
=m+AB+BM . Так как BM = CM , то АС = m + 2AB + CM > m + CM . Это противоречит
неравенству треугольника для ΔAMC : АС < m + CM .
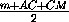
Ответ
нет, не может.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет