Олимпиадная задача по планиметрии: равнобедренный ли треугольник ABC? 8-9 класс

  а) Рассмотрим треугольник ABC, в котором  ∠B = 60°,  ∠A = 45°,  ∠ACB = 75°.

  Отметим на серединном перпендикуляре к стороне AC точку O, для которой  ∠OAC = ∠OCA = 30°  (см. рис.). Пусть луч AO пересекает сторону BC в точке N, а луч CO пересекает сторону AB в точке M. Тогда  ∠ANC = 75°,  ∠OMA = 105°.

  При симметрии относительно серединного перпендикуляра к сторонеACточкаMпереходит в точкуM', лежащую на отрезкеON. При этом ∠OM'C= ∠OMA= 105°,  ∠CM'N= 180° – ∠OM'C= 180° – 105° = 75° = ∠CNM'.   Значит, треугольникCNM'– равнобедренный. Следовательно,  CN = CM' = AM.   Таким образом, неравнобедренный треугольникABCудовлетворяет условию пункта а).   б) Предположим, что  AB < BC.  Пусть серединный перпендикуляр l к стороне AC пересекает прямую BC в точке K (см. рис.). Тогда

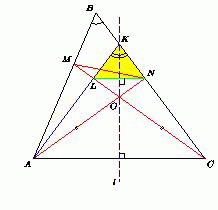
∠KAC = ∠ACK = ∠C < ∠A,  значит, точка K лежит на отрезке BC. Кроме того, поскольку  AO = CO,  то точка O лежит на прямой l. Заметим, что точка L пересечения AK и CM симметрична точке N относительно l. Ясно, что точка L лежит на отрезке MC.

  С другой стороны, поскольку AKC – внешний угол треугольника ABK, то  ∠LKN = ∠AKC > ∠ABK = ∠MBN.

  Значит, угол при вершине равнобедренного треугольника LKN больше угла при вершине равнобедренного треугольника MBN. Поэтому  ∠KNL < ∠BNM,  а это означает, что точка L лежит на продолжении отрезка MC за точку M. Противоречие.

  Аналогично AB не может быть больше BC.

а) Не обязательно;  б) обязательно.