Олимпиадная задача по планиметрии: параллельность отрезка в треугольнике ABC
Задача
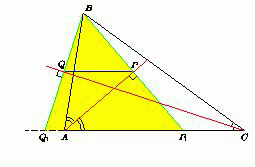
В треугольнике ABC провели биссектрисы углов A и C. Точки P и Q – основания перпендикуляров, опущенных из вершины B на эти биссектрисы. Докажите, что отрезок PQ параллелен стороне AC.
Решение
Пусть точка P лежит на биссектрисе угла A, а точка Q – на биссектрисе угла C. Рассмотрим точки P1 и Q1, симметричные B относительно биссектрис углов A и C. Так как биссектриса – ось симметрии угла, то они лежат на AC. При этом P – середина BP1, а Q – середина BQ1. Следовательно, PQ – средняя линия треугольника P1BQ1, поэтому
PQ || P1Q1 || AC.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет