Олимпиадная задача Шарыгина по планиметрии для 8–9 класса: AN = NC
Задача
Вокруг треугольника ABC описана окружность, к ней через точки A и B проведены касательные, которые пересекаются в точке M. Точка N лежит на стороне BC, причём прямая MN параллельна стороне AC. Докажите, что AN = NC.
Решение
Обозначим ∠MAB = ∠MBA = α. Тогда ∠ACB = α и ∠MNB = ∠ACB = α. Таким образом, из точек N и A, лежащих по одну сторону от прямой BM, отрезок BM виден под одним и тем же углом, равным α. Значит, точки A, N, B и M лежат на одной окружности. Вписанные в эту окружность углы ANM и ABM опираются на одну и ту же дугу, поэтому ∠ANM = ∠ABM = α = ∠ACN, то треугольник ANC – равнобедренный. 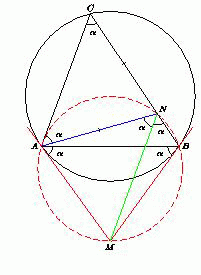
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет