Олимпиадная задача по планиметрии: окружности и касательные параллелограмма
Задача
Диагонали параллелограмма ABCD пересекаются в точке O. Описанная окружность треугольника AOB касается прямой BC.
Докажите, что описанная окружность треугольника BOC касается прямой CD.
Решение
Решение 1:Из теоремы об угле между касательной хордой следует, что ∠CBO= ∠BAO= ∠BAC= ∠ACD= ∠OCD.
По теореме, обратной теореме об угле между касательной и хордой,CD– касательная к окружности, проходящей через точкиB, O, C.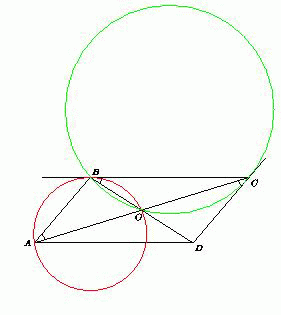
Решение 2:По теореме о секущей и касательной CB² = CA·CO = ½ CA². Из того, что в параллелограмме сумма квадратов сторон равна сумме квадратов диагоналей, отсюда легко выводится равенство DC² = ½ DB² = DB·DO. Таким образом, произведение секущей DB на ее внешнюю часть DO равно квадрату отрезка DC. По той же теореме этот отрезок является касательной.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь