Олимпиадная задача по планиметрии 8-9 класса: медиана в треугольнике и перпендикулярность
Задача
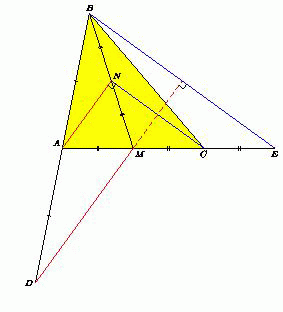
В треугольнике ABC медиана BM равна стороне AC. На продолжениях сторон BA и AC за точки A и C выбраны соответственно точки D и E, причём
AD = AB и CE = CM. Докажите, что прямые DM и BE перпендикулярны.
Решение
Если N – середина медианы BM, то AN и CN – средние линии треугольников DBM и EBM, поэтому AN || DM и CN || BE . В треугольнике ANC медиана NM равна половине стороны AC, поэтому ∠ANC = 90°, следовательно, и DM ⊥ BE.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет