Олимпиадная задача по планиметрии для 8–9 классов: медианы и угол AMB в треугольнике
Задача
В треугольнике ABC медианы AD и BE пересекаются в точке M . Докажите, что если угол AMB а) прямой; б) острый, то AC+BC >3AB .
Решение
Пусть медианы AF и BG треугольника AMB пересекаются в точке N . Поскольку EM = 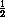 BM = MF , то AM – медиана треугольника AEF . В треугольниках AMF и AME известно, что AM – общая сторона, ME = MF и
BM = MF , то AM – медиана треугольника AEF . В треугольниках AMF и AME известно, что AM – общая сторона, ME = MF и  AMF
AMF 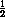
 AME (по условию задачи). Значит, AF
AME (по условию задачи). Значит, AF 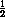 AE =
AE = 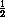 AC . Поэтому
AC . Поэтому
AN = 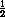 AF
AF 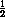
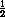 ·
· 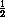 AC =
AC = 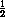 AC.
AC.
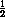
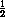 BC .
BC .
По неравенству треугольника AN+BN > AB . Следовательно,
AC+BC 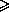 3AN + 3BN = 3(AN+BN) > 3AB.
3AN + 3BN = 3(AN+BN) > 3AB.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет