Олимпиадная задача по планиметрии для 8–9 классов: окружности и перпендикуляры
Задача
Дана окружность с диаметром AB. Другая окружность с центром в точке A пересекает отрезок AB в точке C, причём AC < ½ AB. Общая касательная двух окружностей касается первой окружности в точке D. Докажите, что прямая CD перпендикулярна AB.
Решение
Пусть O – центр первой окружности, E – точка касания второй окружности с общей касательной. Треугольник AOD – равнобедренный, поэтому
∠DAO = ∠ADO, а так как AE || OD (радиусы, проведённые в точку касания), то ∠EAD = ∠ADO = ∠DAO. Треугольники AED и ACD равны по двум сторонам и углу между ними, значит, ∠ACD = ∠AED = 90°.
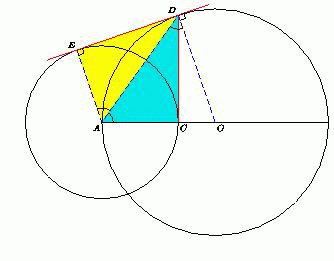
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет