Олимпиадная задача по планиметрии: линейная комбинация векторов в правильном n-угольнике, 8-9 класс
Задача
Из центра O правильного n-угольника A1A2...An проведены n векторов в его вершины. Даны такие числа a1, a2, ..., an, что
a1 > a2 > ... > an > 0. Докажите, что линейная комбинация векторов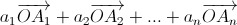 
отлична от нулевого вектора.
Решение
Введём прямоугольную систему координат: начало поместим в центр n-угольника, ось OY направим по прямой OAn; будем для определённости считать, что вершины n-угольника пронумерованы по часовой стрелке. Рассмотрим проекции векторов на ось OX. Множество всех векторов 
разобьём на пары: в одну пару включаем векторы и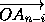 
. На аналогичные пары разобьём числа ai.
В пары войдут все векторы, кроме n-го и, в случае чётного n, вектора с номером n/2. В каждой паре чисел (ai, an–i) при i < n/2 первое число больше второго. Проекции на ось OX векторов и 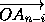равны по модулю и противоположны по знаку. Следовательно, проекция на ось OX линейной комбинации 
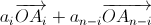положительна. Проекции на ось OX тех векторов, которые не вошли в пары, равны 0. Значит, и проекция всей линейной комбинации на эту ось положительна. Следовательно, эта линейная комбинация отлична от нуля.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь