Олимпиадная задача по планиметрии для 8–10 классов — доказательство OM = KN
Задача
Хорды AC и BD окружности с центром O пересекаются в точке K. Пусть M и N – центры описанных окружностей треугольников AKB и CKD соответственно. Докажите, что OM = KN.
Решение
Рассмотрим проекции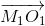 
и 
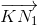векторов 
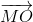и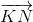 
на хорду AC. N1 – середина хорды KC, поэтому 
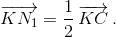M1 и O1 – середины хорд AK и AC, поэтому 
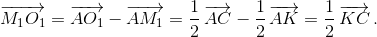Таким образом,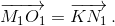 
Аналогично равны проекции векторов 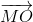и 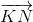на хорду BD. Но вектор полностью определяется своими проекциями на две непараллельные прямые. Поэтому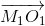 
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет