Олимпиадная задача: Ладья на шахматной доске — алгоритмы и доказательство

  Случай  m = n = 1  очевиден (первому некуда ходить).

  Далее будем считать, что  m ≤ n,  n > 1,  а ладья вначале стоит в левом верхнем углу.

  Оказывается, первому достаточно все время делать наиболее длинные ходы. Докажем правильность этой стратегии от противного. Предположим, что существует доска, на которой эта стратегия не приводит к выигрышу, и рассмотрим среди них доску m×n наименьшей площади. Очевидно,  m > 1.

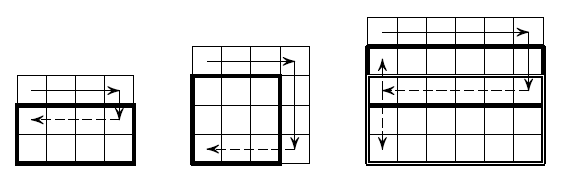
  Первый ходит по длинной стороне (горизонтали) до конца. Второй вынужден сделать ход в перпендикулярном направлении. Рассмотрим три случая.

  1) Второй пошёл на одну клетку. Тогда игра сводится к аналогичной для доски  (m–1)×n  (рис. слева). Поскольку  m ≥ 2,  доска 1×1 не получится.

  2) Второй пошёл до конца. Если  m = n= 2,  то первый сразу выигрывает. В противном случае игра будет происходить так же, как если бы первый начал игру на доске  (m–1)×(n–1)  (рис. в центре).   3) Второй пошёл наkклеток,  1 <k < m– 1.  Тогда  m≥ 3.  Первый пойдёт до конца по горизонтали. Если второй после этого пойдет вверх, то вся дальнейшая игра будет происходить, как на доске  k×(m–1),  где уже сделано два первых хода. Доска 1×1 не получится, так как  n– 1 ≥ 2  (рис. справа).   Если второй пойдет вниз, то вся дальнейшая игра будет происходить, как на доске  (m–k)×n,  где уже сделано два первых хода.   В любом случае игра будет идти, как если бы она началась двумя ходами позже на меньшей доске, отличной от 1×1. Но на этой доске стратегия верна. Значит, она верна и на исходной доске. Противоречие.

Начинающий (на всех досках, кроме 1×1).