Олимпиадная задача по классической комбинаторике для 7-9 класса от Токарева С.И.
Задача
a) Восемь школьников решали восемь задач. Оказалось, что каждую задачу решили пять школьников. Докажите, что найдутся такие два школьника, что каждую задачу решил хотя бы один из них.
б) Если каждую задачу решили четыре ученика, то может оказаться, что таких двоих не найдётся.
Решение
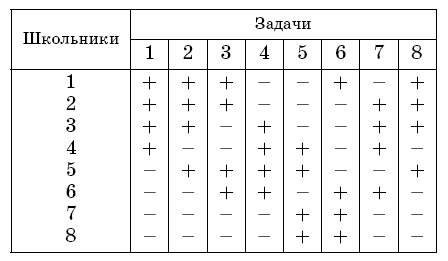
a) Будем тройку из двух учеников и задачи, которую они оба не решили, называть отмеченной. Поскольку каждую задачу не решили трое учеников, каждой задаче соответствуют три отмеченные тройки. Значит, всего отмечено 24 тройки. С другой стороны, имеется 7·8 : 2 = 28 пар учеников. Следовательно, есть пара учеников, не входящая ни в одну в отмеченную тройку. Это и значит, что они решили все задачи. б) Пример:
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь