Олимпиадная задача по планиметрии и инвариантам: четыре прямоугольных треугольника, 8-10 класс

Решение 1:   Заметим, что порядок, в котором разрезали треугольники, не важен: конечный результат от этого не зависит.

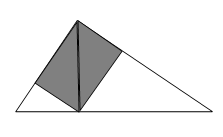
  Предположим, что после некоторого числа разрезаний получились попарно различные треугольники. Поскольку первоначально имеется четыре одинаковых треугольника, три из них были разрезаны. Сделаем сначала эти три разреза. В результате образовались две тройки одинаковых треугольников. В каждой из этих троек были разрезаны хотя бы по два треугольника. Сделаем эти разрезы. После этого у нас опять образуются четыре одинаковых треугольника (см. рис.). Три из них придётся разрезать... Итак, мы видим, что процесс никогда не кончится. Противоречие.

Решение 2:   Пусть гипотенузы исходных треугольников равны 1, а их катеты – p и q. Тогда все получаемые разрезаниями треугольники подобны исходному с коэффициентом вида p^mqⁿ (m и n – целые неотрицательные числа). При разрезании такого треугольника получаются два – подобные исходному с коэффициентами и p^m+1qⁿ и p^mqⁿ⁺¹. Теперь задачу можно переформулировать так.

  На координатной плоскости, разбитой на единичные клетки, в вершине положительного квадранта стоят четыре фишки. Любую фишку можно заменять на две соседние (сверху и справа). Докажите, что нельзя добиться того, чтобы все фишки стояли в разных клетках.

  Присвоим каждой клетке вес, как в решении задачи 197775. Тогда суммарный вес всех фишек не меняется. Но в начальный момент он равен 2, а сумма весов любого конечного числа фишек, стоящих в разных клетках, как показано в том же решении, меньше двух.

Ответ задачи отсутствует