Олимпиадная задача: Хорды и равновеликие части в многоугольнике — планиметрия, 9–11 классы

  а) Примером служит многоугольник, состоящий из трёх одинаковых квадратов (залов), соединенных тонкими изогнутыми коридорами (см. рис.).

  ПустьS– площадь многоугольника, 0,3S– площадь одного зала (0,1S– суммарная площадь всех коридоров). Если хорда пересекает только коридор, то по одну сторону от нее расположены два зала, и их площадь больше половины площади многоугольника. Если хорда пересекает один из залов, то она не пересекает "перекрестка" трёх коридоров, а тогда опять в одной части расположены два зала.   б) Выберем направление хорды, не параллельное сторонам и диагоналям многоугольника, и будем считать это направление вертикальным. Тогда хорда может проходить не более чем через одну вершину многоугольника. Если ни одна внутренняя точка хорды не является вершиной многоугольника, то хорда делит многоугольник ровно на 2 части, в противном случае – ровно на 3.

  Если площадь меньшей части больше или равна ^S/₃, то задача решена. В противном случае, будем двигать хорду перпендикулярно вертикали в ту сторону, в которую площадь меньшей части многоугольника растёт. При движении хорда может "натолкнуться" на внутреннюю вершину (но не на две вершины сразу).

  Если хорда не встречает препятствий на своем пути, площадь наименьшей части изменяется непрерывно.   Если в какой-то момент она достигнет ^S/₃, то задача решена. В противном случае, хорда натолкнется на внутреннюю вершину. В этом месте могут сходиться или расходиться два коридора (рис. слева), тогда хорда, выходя из коридора, скачком увеличится или, входя в коридор, скачком уменьшится (или "перепрыгнет" в другую часть многоугольника, как на рис. справа).

  Из трёх образовавшихся частей многоугольника самая большая должна иметь площадь больше ^S/₃. Направим вертикальную хорду в наибольшую часть, тогда две меньшие части объединятся. Если их площадь станет больше или равна ^S/₃, то задача решена. В противном случае продолжаем двигать хорду, пока она не натолкнется на следующую вершину, и т. д.

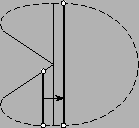
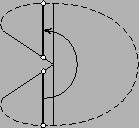
  Площадь меньшей части всё время растёт, поэтому мы не можем пройти два раза через одну и ту же внутреннюю вершину. Но внутренних вершин – конечное число, значит, процесс завершится.

Ответ задачи отсутствует